Pin điện thoại di động và máy tính bảng là một trong những mối quan tâm hàng đầu của người dùng hiện nay. Bạn có bao giờ tự hỏi thời gian sử dụng màn hình thực sự ảnh hưởng đến dung lượng pin như thế nào? Liệu có một mối quan hệ rõ ràng, có thể định lượng được giữa hai yếu tố này không? Trong vai trò là một chuyên gia về công nghệ và phân tích dữ liệu, tôi đã tìm thấy câu trả lời thông qua việc ứng dụng Python và các công cụ thống kê mạnh mẽ của nó. Bài viết này sẽ hướng dẫn bạn cách thực hiện một phân tích tương tự, giúp bạn hiểu sâu hơn về thiết bị của mình.
Gần đây, tôi muốn khám phá cách thời gian bật màn hình trên điện thoại và máy tính bảng đang ảnh hưởng đến mức hao hụt pin. Mặc dù bạn có thể không nghĩ ngay đến Python cho mục đích này, nhưng các công cụ thống kê cơ bản của nó thực sự có thể cung cấp câu trả lời chính xác và đáng tin cậy.
Câu Hỏi Nghiên Cứu: Thời Gian Bật Màn Hình Ảnh Hưởng Đến Pin Như Thế Nào?
Có lẽ tôi là một trong số những người thường xuyên lo lắng về tuổi thọ pin, mặc dù thực tế tôi không cần phải như vậy. Với cả điện thoại Android và máy tính bảng, tôi luôn có đủ pin vào cuối ngày, và làm việc tại nhà, tôi không bao giờ ở quá xa ổ cắm điện.
Việc màn hình bật sẽ tốn pin hơn là điều hiển nhiên, nhưng tôi tò mò về mối quan hệ thực sự giữa chúng. Liệu đây có phải là một mối quan hệ tuyến tính, nghĩa là mức tiêu thụ pin tăng theo một tỷ lệ cố định với thời gian bật màn hình? Hay nó có thể là một mối quan hệ lũy thừa, nơi việc sử dụng pin tăng nhanh chóng khi thời gian màn hình kéo dài?
Tôi đã rất hứng thú với phân tích dữ liệu gần đây. Sau khi tham gia một khóa học về thống kê và xác suất cơ bản ở đại học, tôi đã lần đầu tiên tiếp xúc với khái niệm hồi quy tuyến tính, nơi các điểm dữ liệu được vẽ trên hai trục và một đường thẳng được vẽ xuyên qua chúng, trong một phòng thí nghiệm vật lý.
Khi tôi nhận thấy cả điện thoại và máy tính bảng của mình đều lưu giữ số liệu thống kê về thời gian bật màn hình và mức sử dụng pin, tôi đã nhớ lại kinh nghiệm trước đây của mình. Chiếc máy tính bỏ túi TI tôi từng dùng ở đại học — giờ nằm đâu đó trong nhà — nhưng tôi không còn cần nó nữa vì đã có Python. Tôi quyết định sử dụng bộ công cụ tính toán thống kê phong phú của Python để tìm hiểu mối quan hệ, nếu có, giữa thời gian bật màn hình và tuổi thọ pin.
Thiết Lập Giả Thuyết Nghiên Cứu Khoa Học
Một phần quan trọng của thống kê là kiểm định giả thuyết. Đây là chìa khóa cho khoa học tốt. Mặc dù có thể hơi “quá mức cần thiết” cho một dự án nhỏ như thế này, nhưng tôi muốn trở thành một nhà thống kê và nhà khoa học tốt, dù chỉ trong một thời gian ngắn.
Trong thống kê, bạn sẽ hình thành một giả thuyết null (H0) và một giả thuyết thay thế (H1).
Giả thuyết null (H0) thường là điều bạn muốn bác bỏ. Nếu bằng chứng dưới dạng một kiểm định thống kê cho phép, bạn sẽ chọn giả thuyết thay thế (H1).
Trong trường hợp thời gian bật màn hình và tuổi thọ pin của điện thoại và máy tính bảng của tôi:
| Giả thuyết Null (H0) | Không có mối quan hệ giữa thời gian bật màn hình và tuổi thọ pin. |
|---|---|
| Giả thuyết Thay thế (H1) | Có mối quan hệ giữa thời gian bật màn hình và tuổi thọ pin. |
Với các giả thuyết null và thay thế đã được định nghĩa, tôi có thể tiến hành thu thập và phân tích dữ liệu của mình.
Thu Thập và Nhập Dữ Liệu Pin Vào Python
Bước đầu tiên là sắp xếp dữ liệu của tôi. Hệ điều hành Android được tùy chỉnh trên điện thoại và máy tính bảng Samsung của tôi theo dõi mức sử dụng pin và thời gian bật màn hình trong tuần qua.
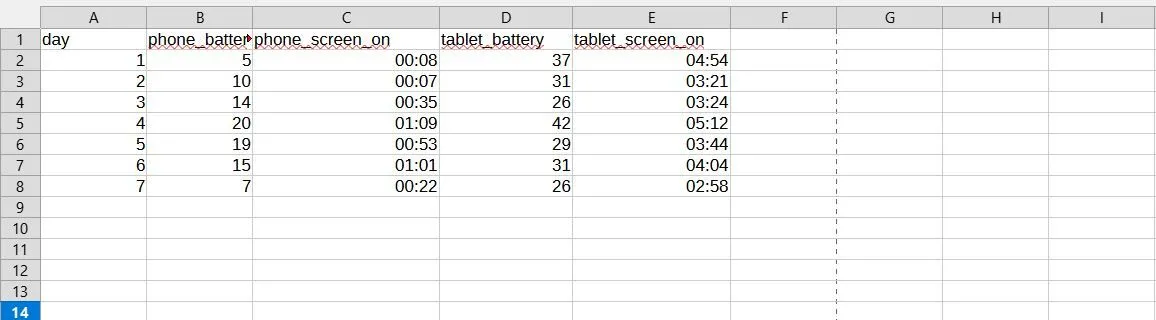Dữ liệu thống kê pin điện thoại và máy tính bảng được tổ chức trong bảng tính LibreOffice Calc
Tôi cẩn thận mở trang chẩn đoán trên máy tính bảng và điện thoại của mình, sao chép dữ liệu vào bảng tính LibreOffice Calc, sau đó lưu nó dưới dạng tệp CSV.
Tôi đã tạo các cột cho thời gian bật màn hình được báo cáo của điện thoại và máy tính bảng, với hai cột cho mỗi thiết bị. Tôi nghĩ cách dễ nhất để mã hóa thời gian bật màn hình là nhân số giờ với 60 và cộng thêm số phút, cho tổng số phút màn hình điện thoại được bật. (Ban đầu tôi đã mã hóa chúng dưới dạng giờ và phút trong bảng tính, nhưng thư viện pandas dường như không thích định dạng đó, vì vậy cuối cùng tôi đã mã hóa lại.)
Tôi đã sử dụng thư viện pandas của Python để đọc dữ liệu. pandas có thể đọc nhiều định dạng dữ liệu, bao gồm tệp CSV. pandas giúp dễ dàng làm việc với dữ liệu được sắp xếp theo hàng và cột, giúp việc chuyển từ bảng tính sang Python trở nên thuận tiện.
Tôi mở một Jupyter notebook và chạy một số lệnh Python để thiết lập môi trường:
import numpy as np
import pandas as pd
import seaborn as sns
import pingouin as pg
%matplotlib inline
Không gian vũ trụ với laptop hiển thị logo Jupyter và hành tinh Sao Mộc
Các lệnh này thiết lập các thư viện tôi sẽ sử dụng. NumPy rất hữu ích cho mọi loại phép toán số, bao gồm thống kê. Nó giống như một “chiếc chăn an toàn” thống kê, vì vậy tôi luôn nhập nó bất cứ khi nào tôi làm việc với dữ liệu. Câu lệnh thứ hai hiển nhiên nhập pandas, nhưng viết tắt là “pd” để tôi không phải liên tục gõ “pandas.” Seaborn là một công cụ tuyệt vời để tạo các biểu đồ thống kê, và đó là những gì tôi đã sử dụng để tạo các biểu đồ phân tán và hồi quy của mình. Pingouin (tiếng Pháp có nghĩa là “chim cánh cụt”) là một thư viện thực hiện các kiểm định thống kê, và đó là những gì tôi đã sử dụng để xây dựng các mô hình của mình và xem mức độ phù hợp của chúng với dữ liệu.
Dòng cuối cùng trong khối đó là để làm cho bất kỳ biểu đồ nào xuất hiện trực tiếp trong Jupyter notebook. Nếu không, chúng sẽ xuất hiện trong một cửa sổ riêng biệt.
Với tất cả các thư viện cần thiết đã được tải, tôi có thể tạo một dataframe của pandas với dữ liệu của mình:
battery = pd.read_csv("data/device_batteries.csv")Tôi có thể kiểm tra dataframe mới của mình bằng hàm head():
battery.head()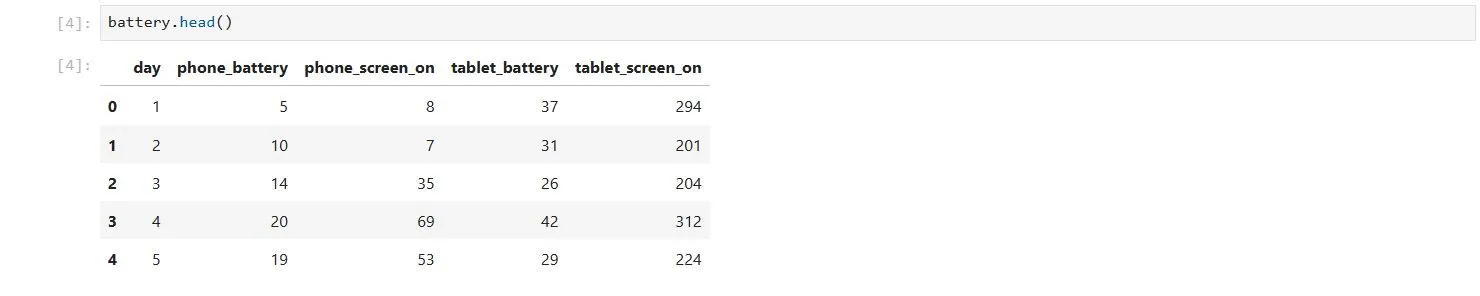
Kết quả đầu ra lệnh battery.head() sử dụng thư viện Pandas trong Python, hiển thị các dòng dữ liệu pin
Lệnh này hiển thị một vài dòng đầu tiên của dữ liệu và cho phép tôi xem cách nó được tổ chức. Tất nhiên, tôi đã biết điều đó vì tôi đã tự tạo nó. Lệnh này đặc biệt hữu ích cho bất kỳ tập dữ liệu nào tôi tải xuống từ các nguồn như Kaggle.
Bước tiếp theo là lấy một số thống kê mô tả từ tập dữ liệu của tôi. Phương thức describe() của dataframe thực hiện chính xác điều đó:
batteries.describe()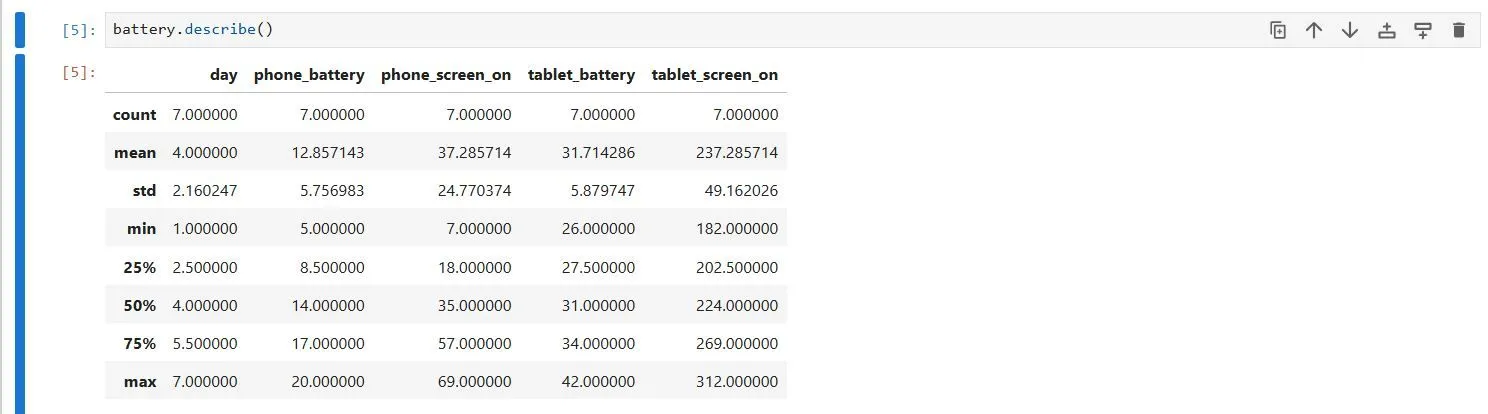
Thống kê mô tả dữ liệu pin trong Python, được tạo bằng hàm describe() của thư viện Pandas
Lệnh này in ra các thống kê mô tả cơ bản như số lượng (count), giá trị trung bình (mean), độ lệch chuẩn (standard deviation), giá trị nhỏ nhất và lớn nhất (min và max), cũng như phân vị thứ 25 (lower quartile), trung vị (median – phân vị thứ 50) và phân vị thứ 75 (upper quartile) cho tất cả các cột số trong dataframe. Tất cả các thống kê này giúp tôi có cái nhìn tổng quan về tập dữ liệu.
Biểu Diễn và Phân Tích Hồi Quy Tuyến Tính Bằng Seaborn và Pingouin
Sau khi dữ liệu đã được nhập và chuẩn bị, đã đến lúc khám phá các mối quan hệ tiềm ẩn.
Khảo Sát Mối Quan Hệ Trên Điện Thoại
Tôi bắt đầu bằng cách tạo biểu đồ phân tán giữa thời gian bật màn hình điện thoại và mức tiêu thụ pin theo phần trăm:
sns.relplot(x='phone_screen_on',y='phone_battery',data=battery)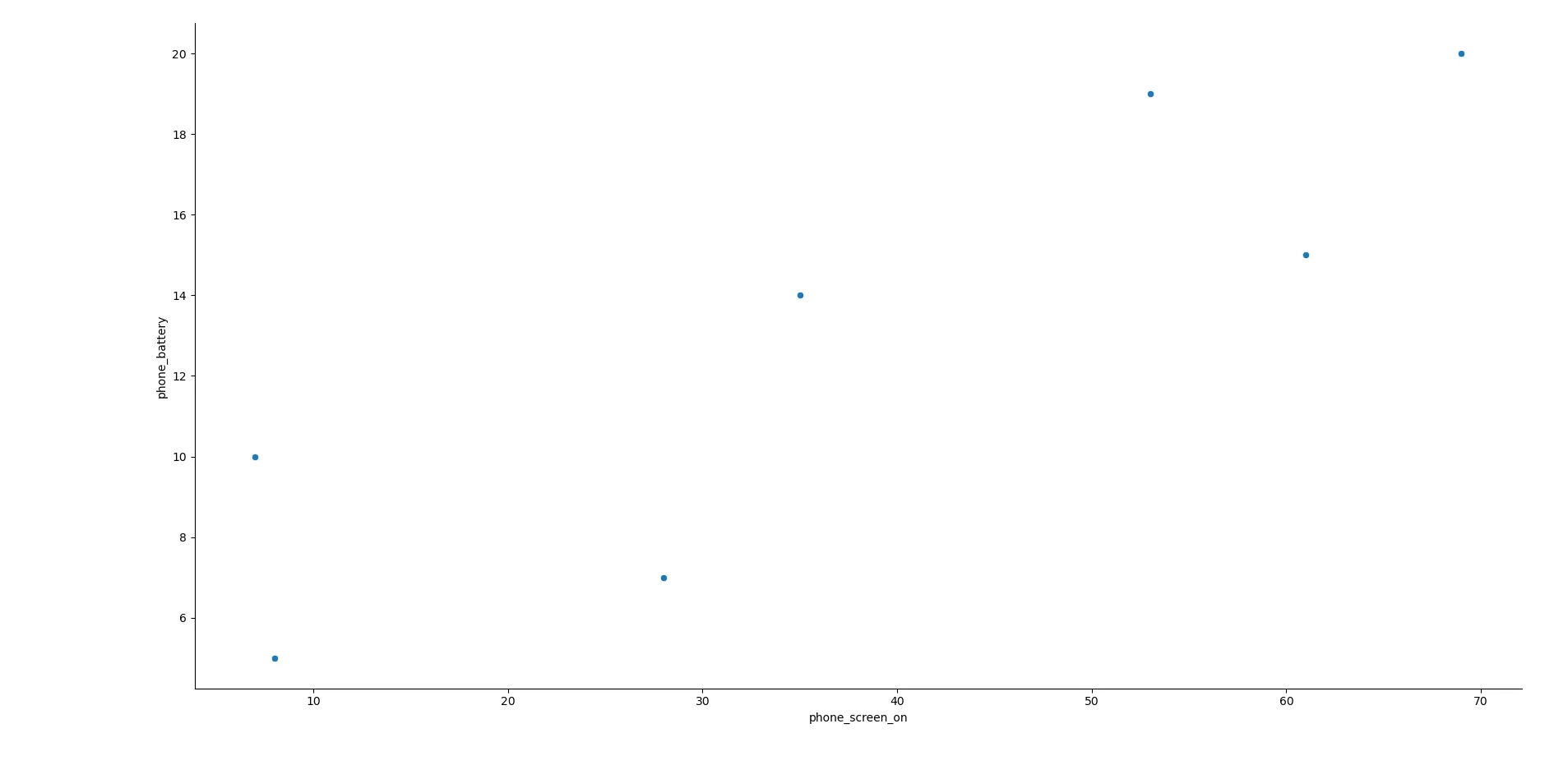
Biểu đồ phân tán thể hiện mối quan hệ giữa thời gian bật màn hình điện thoại và mức tiêu thụ pin, được tạo bằng Seaborn
Biểu đồ này hướng dẫn Seaborn tạo một biểu đồ với thời gian bật màn hình làm trục x và mức tiêu thụ pin làm trục y. Nếu bạn nhìn kỹ, các điểm dữ liệu dường như gần như thẳng hàng. Tôi quyết định vẽ đường hồi quy và xem mức độ phù hợp của một đường thẳng:
sns.regplot(x='phone_screen_on',y='phone_battery',data=battery)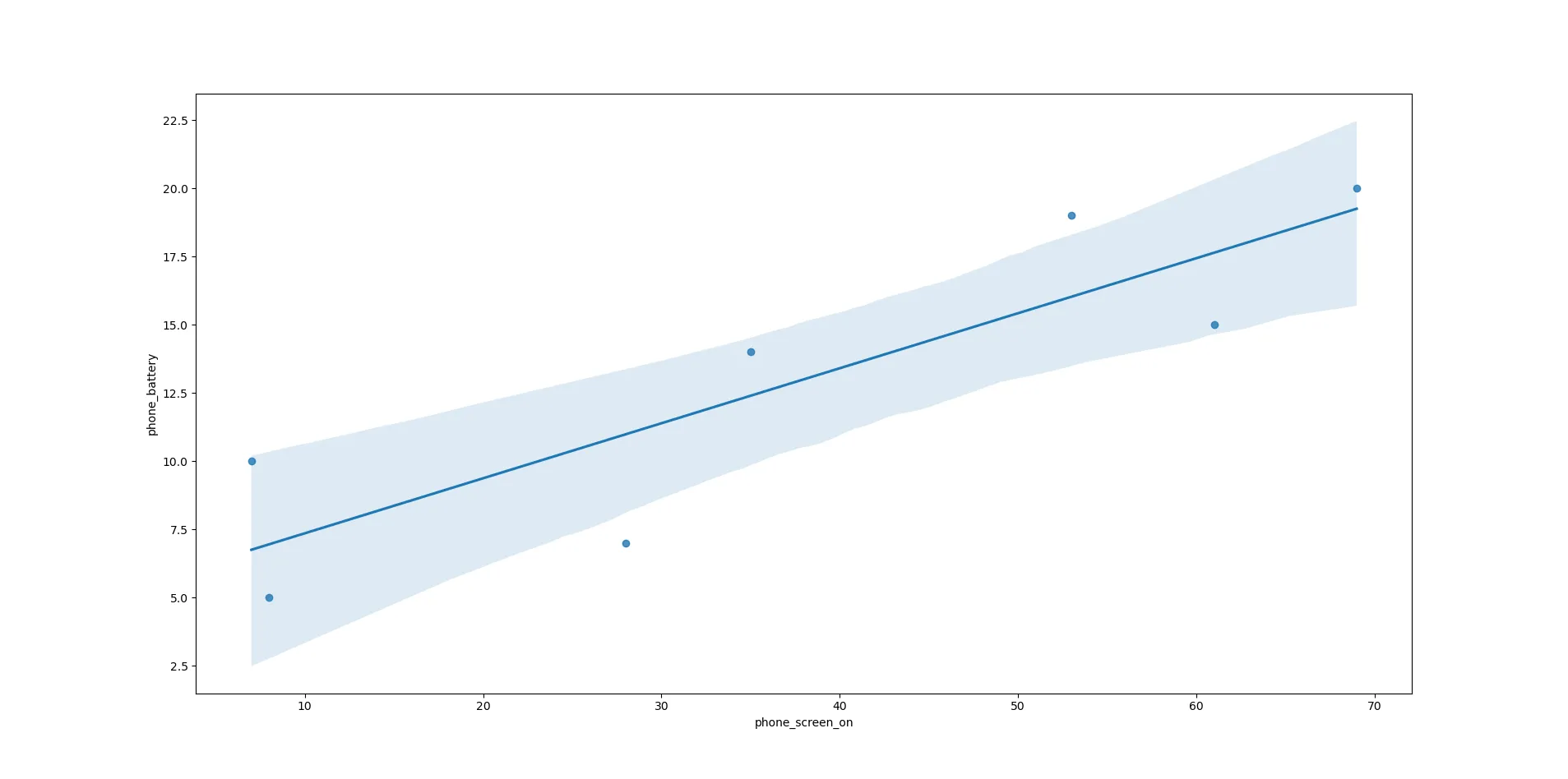
Biểu đồ hồi quy tuyến tính giữa thời gian bật màn hình điện thoại và mức độ hao hụt pin, được vẽ bằng Seaborn
Đường thẳng này khá phù hợp với dữ liệu.
Nhưng làm thế nào để xác minh mức độ phù hợp và làm thế nào để xây dựng lại phương trình đã được sử dụng để tạo ra đường thẳng này? Đó là lúc Pingouin phát huy tác dụng. Một số thư viện khác cho phép bạn thực hiện các kiểm định thống kê và tạo hồi quy, nhưng Pingouin là lựa chọn yêu thích của tôi vì tôi thấy nó dễ sử dụng nhất.
Tôi đã sử dụng hàm hồi quy tuyến tính của Pingouin trên thời gian bật màn hình so với mức tiêu thụ pin:
pg.linear_regression(battery['phone_screen_on'],battery['phone_battery'])
Bảng kết quả hồi quy pin từ thư viện Pingouin, hiển thị các hệ số và giá trị thống kê
Pingouin tạo ra một bảng kết quả. Dưới đây là ý nghĩa của nó. Các con số thực sự quan trọng nằm ở phía bên trái. Nếu bạn nhớ đại số, phương trình của một đường thẳng là y = mx + b. Với hồi quy tuyến tính, chúng ta thay đổi một chút để tạo ra một “phương trình chuẩn” là y = b + mx, hay đúng hơn là y = a + bx. Giao điểm y, hay nơi đường thẳng cắt trục y, là giá trị a, được dán nhãn “intercept” là 5.339232. Hệ số của x, hay thời gian bật màn hình, là 0.201630, xác định độ dốc của đường thẳng. Vì vậy, phương trình của mô hình của chúng ta là y = 5.339232 + 0.201630x.
Các con số khác cho chúng ta biết mức độ phù hợp của đường thẳng này. “se” là viết tắt của “standard error” (lỗi chuẩn) và đo lường khoảng cách trung bình của các điểm dữ liệu so với đường thẳng. Lỗi chuẩn càng thấp, mô hình càng phù hợp. Đối với thời gian bật màn hình, giá trị này khoảng 0.20, có nghĩa là đường thẳng này phù hợp tốt với các điểm dữ liệu. Chỉ số T (T score) là thống kê t của kiểm định t của Student, đo lường kiểm định giả thuyết rằng hệ số tương quan (được đề cập dưới đây) là 0, nghĩa là không có tương quan. Giá trị lớn hơn 2 hoặc nhỏ hơn -2 có nghĩa là kết quả có ý nghĩa thống kê. Giá trị p (p-value) là xác suất mà thống kê mẫu, trong trường hợp này là giá trị t, sẽ cực đoan hoặc cực đoan hơn nếu giả thuyết null là đúng. Hầu hết các nhà thống kê sử dụng một ngưỡng nhất định, thường là tối đa 0.05, để chấp nhận hoặc bác bỏ giả thuyết null. Bởi vì thống kê t lớn hơn 2 và giá trị p nhỏ hơn 0.05, chúng ta có thể bác bỏ giả thuyết null rằng không có mối quan hệ giữa thời gian bật màn hình và mức tiêu thụ pin ở cả mức ý nghĩa 0.05 và 0.01.
Các giá trị “r2” và “r2_adjusted” là bình phương của hệ số tương quan. Giá trị cao ở đây cũng có nghĩa là đường thẳng phù hợp tốt. Hai cột cuối cùng là khoảng tin cậy (confidence intervals), đại diện cho các khu vực mà các giá trị của phương trình có thể nằm trong mức độ tin cậy 2.7% và 97.5%. Các vùng bóng mờ trong biểu đồ hồi quy cũng đại diện cho các khoảng tin cậy.
Bây giờ chúng ta đã có một mô hình, chúng ta có thể cắm các giá trị vào biến thời gian bật màn hình để dự đoán mức tiêu thụ pin.
Tôi có thể định nghĩa một hàm Python cho việc này:
def phone_battery_usage(minutes):
return 5.339232 + 0.201630 * minutesĐể tính mức sử dụng cho ba giờ hoặc 180 phút:
phone_battery_usage(180)Khảo Sát Mối Quan Hệ Trên Máy Tính Bảng
Hãy làm điều tương tự cho máy tính bảng của tôi. Đầu tiên là biểu đồ phân tán:
sns.relplot(x='tablet_screen_on',y='tablet_battery',data=battery)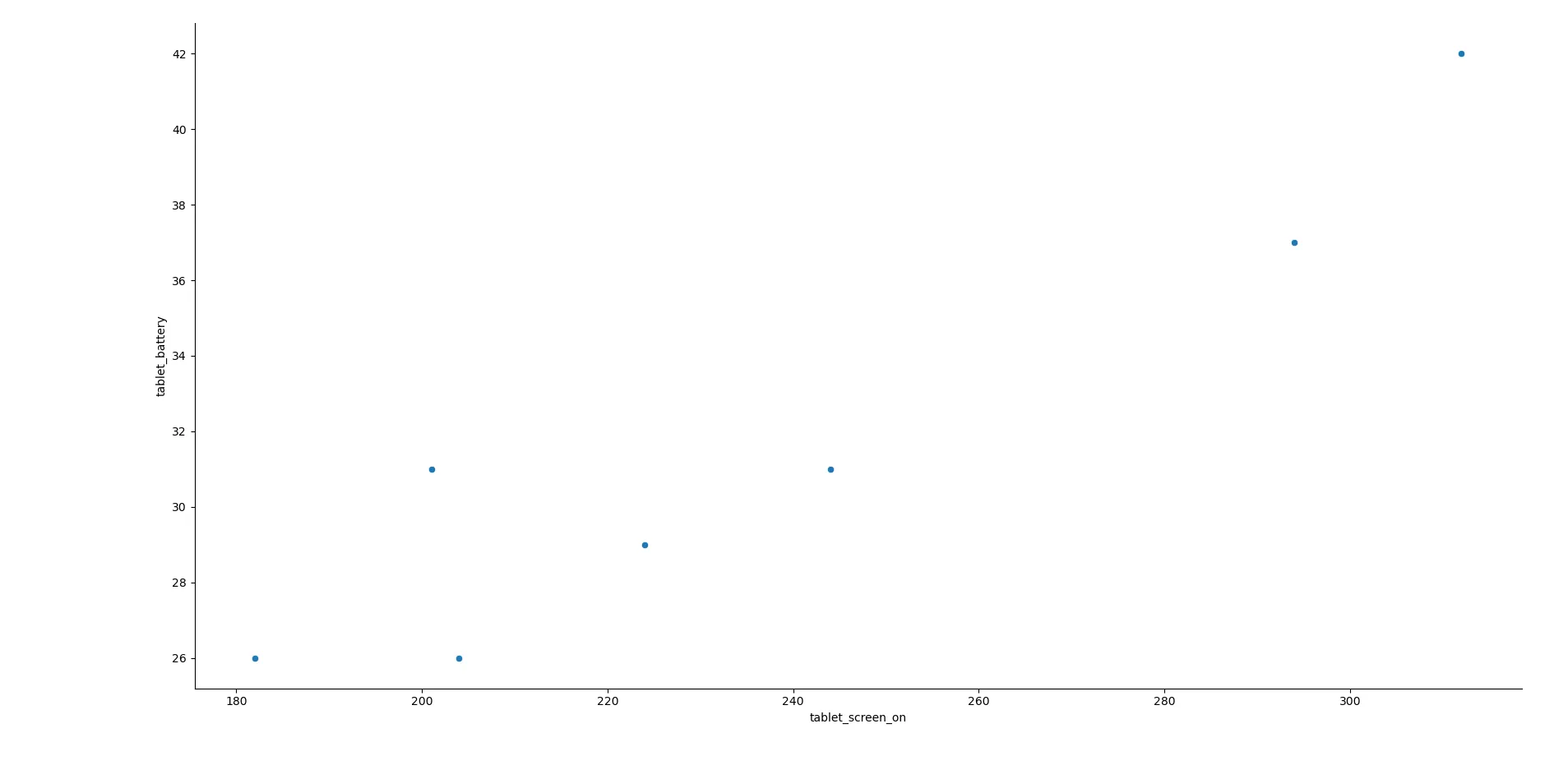
Biểu đồ phân tán thể hiện thời gian bật màn hình máy tính bảng so với mức tiêu thụ pin
Một lần nữa, dường như có một mối tương quan tuyến tính. Hãy vẽ đường hồi quy:
sns.regplot(x='tablet_screen_on',y='tablet_battery',data=battery)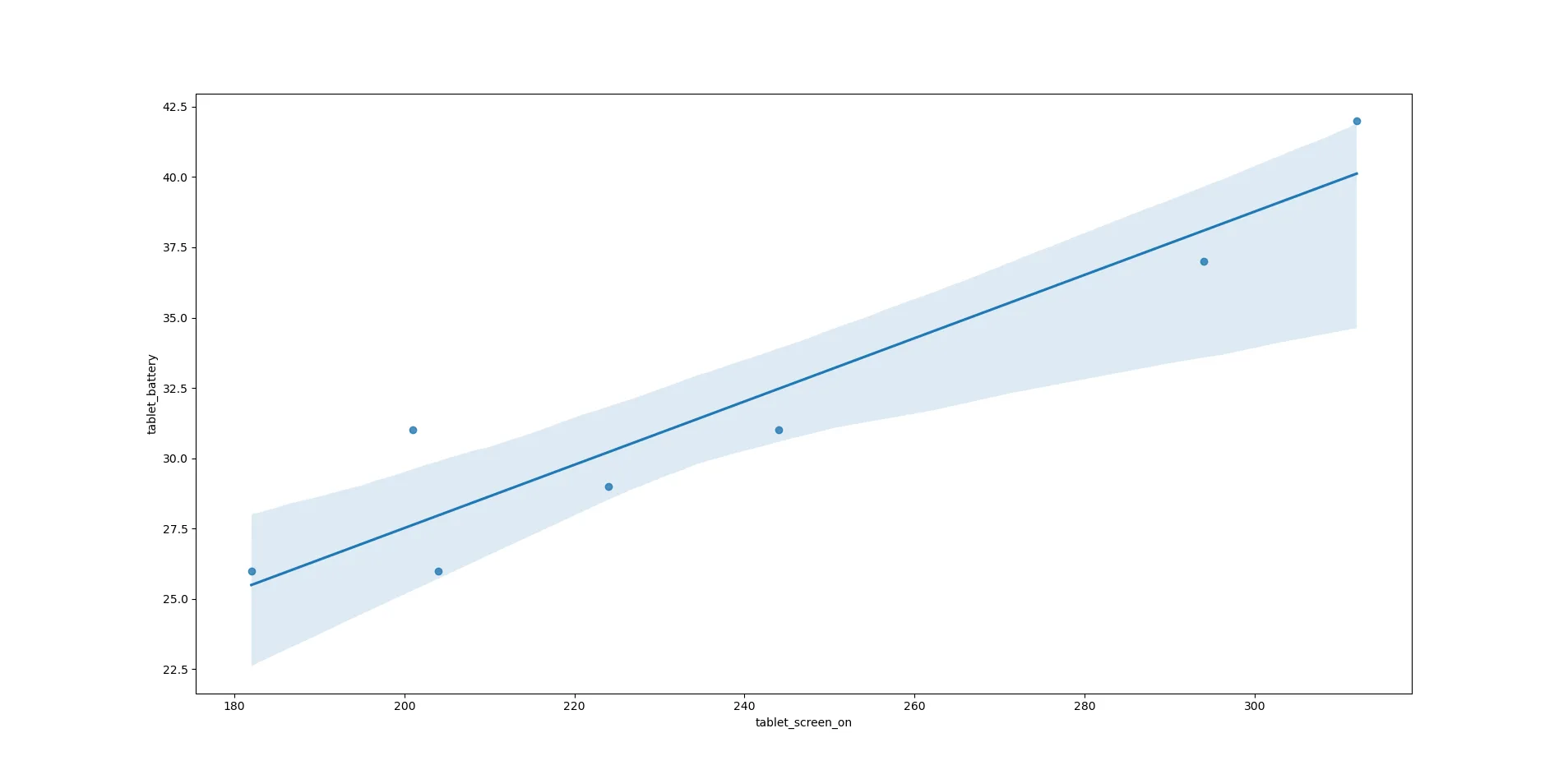
Biểu đồ hồi quy tuyến tính của thời gian bật màn hình máy tính bảng và mức tiêu thụ pin, được tạo bằng Seaborn
Một sự phù hợp tốt khác. Hãy thử một hồi quy tuyến tính Pingouin:
pg.linear_regression(battery['tablet_screen_on'],battery['tablet_battery'])
Bảng kết quả hồi quy Pingouin cho mối quan hệ giữa thời gian bật màn hình máy tính bảng và mức tiêu thụ pin
Mô hình cho máy tính bảng là *mức tiêu thụ pin = 5.017013 + 0.112511 (thời gian bật màn hình)**. Đây là một sự phù hợp tốt, với T = 6.202436, p = 0.001591 và r² = 0.884979.
Những Bài Học Rút Ra Từ Dự Án Phân Tích Pin
Một điều khiến tôi ngạc nhiên là cách các mối quan hệ tuyến tính vẫn tồn tại trong thế giới thực. Mức sử dụng pin là tuyến tính cho cả điện thoại và máy tính bảng của tôi. Điều này có thể phù hợp với một số nghiên cứu tôi đã thực hiện về mức tiêu hao pin của pin lithium-ion, nơi chúng tiêu hao nhanh hơn khi bạn bắt đầu sử dụng và về cuối chu kỳ sạc, nhưng đường cong xả vẫn tuyến tính ở giữa, theo Ufine Battery. Dự án này chứng minh giá trị thực tiễn của phân tích thống kê trong công nghệ.
Nó cung cấp một cách nghiêm ngặt hơn để trả lời các câu hỏi, nhưng với phần mềm hiện đại như Python, Seaborn và Pingouin, việc khám phá các vấn đề phức tạp trở nên dễ dàng hơn bao giờ hết đối với các nhà nghiên cứu và những người bình thường như tôi. Hi vọng qua bài viết này, bạn cũng đã có thêm một góc nhìn thú vị về cách ứng dụng Python để giải mã các thông số công nghệ hàng ngày.
Bạn có muốn tự mình thử phân tích dữ liệu pin trên thiết bị của mình không? Hãy chia sẻ kinh nghiệm hoặc câu hỏi của bạn trong phần bình luận bên dưới nhé!